Criptografía simétrica

“Curso de Introducción a la Criptografía” by Jordi Íñigo Griera is licensed under a
Creative Commons Attribution 4.0 International License.
Project hosted at github.com/jig/crypto

Criptografía simétrica

hace falta que sea segura y práctica

el problema es que el requisito definido hasta ahora de confidencialidad perfecta no puede generar cifrados prácticos
(ya que $\|k\| = \|m\|$)

Confidencialidad perfecta

aquella que, a partir del texto cifrado, no permite deducir
ninguna propiedad
del texto original en claro,
aunque el atacante tenga capacidad computacional infinita

Confidencialidad computacional

habitualmente no nos hará falta confidencialidad perfecta, sino que podemos admitir un cierto riesgo de que el sistema/algoritmo no sea confidencial (seguro) frente a un atacante que tenga recursos computacionales finitos

esta "cesión" la haremos a cambio de tener algoritmos más prácticos:

$\|k\| \ll \|m\|$

Confidencialidad computacional

por ejemplo supongamos que tenemos $k$ y $m$ de las longitudes siguientes:

$\begin{aligned} \|k\| &= 128 \\ \|m\| &= 8·10^{6} \end{aligned}$

es decir, tenemos un número de posibles $k$ y $m$:

$\begin{aligned} |k| &= 2^{128} = 340282366920938463463374607431768211456 \\ |m| &= 2^{8·10^{6}} = 923234126834\cdots \\ |c| &= 2^{8·10^{6}} = 923234126834\cdots \end{aligned}$

Confidencialidad computacional

la desproporción entre $|k|$ y $|c|$ hace que sólo una de las claves devuelva un mensaje inteligible, por tanto, podemos saber cual era la clave y el mensaje

si la encontramos

Confidencialidad computacional

si el espacio de claves es suficientemente grande ($|k|$) no podremos probarlas todas
(Muchas claves y Vigenère: espacio de claves)

podemos probar $10^6$ clave/CPU/s $\approx 2^{20}$ clave/CPU/s

ó $10^{13}$ clave/CPU/año $\approx 2^{43}$ clave/CPU/año

ó $10^{16}$ clave/año con $1000$ CPU $\approx 2^{53}$ clave/año

Google's SHA1tered experiment: $6500$ CPU·año

ó $10^{19}$ clave/año con $10^6$ CPU $\approx 2^{63}$ clave/año
$\vdots$

$\vdots$
ó $10^{25}$ claves con $10^6$ CPU un millón de años $\approx 2^{83}$ clave

ó $10^{29}$ claves con $10^6$ CPU desde el Big Bang $\approx 2^{96}$ clave
$\vdots$

si tengo una "suerte media" sólo nos hará falta la mitad de las pruebas (e.g. en el último escenario necesitaremos "sólo" la mitad de la edad del Universo para encontrar la clave)

Confidencialidad computacional

con hardware ad-hoc podemos llegar a multiplicar por $10^4$/$10^5$ veces
($2^{13}$/$2^{17}$ veces)

Ejemplo BitCoin: SHA-256 en hardware masivamente paralelo

Espacio de claves

En criptografía simétrica usaremos algoritmos de cifrado sobre los que el mecanismo más eficiente para un atacante será probar todas las claves hasta encontrar la buena

NIST

el NIST recomienda (2015) claves en las que un atacante
tenga que hacer $2^{112}$ pruebas

Más exactamente, dice que las claves han de tener una longitud
$\|k\| = 112$ b, mínimo

A partir del 2030 prevé recomendar $\|k\| = 128$ b, mínimo

Security Strength son los bits de seguridad o seguridad equivalente
Son necesarias como mucho $2^{\text{security strength}}$ operaciones
para "romper" un algoritmo

NIST: National Institute of Standards and Technology (EE.UU.)

Security Strength

Si la Security Strength implica los mismos bits que un ataque de fuerza bruta (o no muchos menos), diremos que ese algoritmo es "seguro"

la criptografia simétrica (segura) ofrece una security strength igual a la longitud de la clave. En otras primitivas, la security strength es menor a la longitud de la clave.

Cuantificación de la Seguridad

el NIST recomienda las siguientes longitudes de clave (security strength) para los próximos años

112 bit: hasta 2030; 3DES es suficiente
128 bit: a partir de 2030; AES-128 es suficiente

la amenza conocida que puede modificar el calendario es la computación cuántica $\Rightarrow$ AES-256

Criptografía simétrica

hay dos tipos de cifrado simétrico

Cifrados de flujo
Cifrados de bloque

ambos los podemos ver como una evolución de los
bloques de un solo uso:

los primeros "generando" la clave
los segundos aplicándolo varias veces (aprox)

Cifrado de flujo

Es una implementación práctica de los bloques
de una solo uso (one-time-pad)

en el caso de los bloques de un solo uso necesitábamos
$\|k\| = \|m\|$

para después hacer:
$c = k \oplus m$

Cifrado de flujo

lo que haremos es generar una $k_{\text{generada}}$...

$\|k_{\text{generada}}\| = \|m\|$

...a partir de una clave $k$ de longitud corta:

$k \overset{f}{\longrightarrow} k_{\text{generada}}$

para después hacer:
$c = k_{\text{generada}} \oplus m$

$k \xrightarrow{\text{PRNG}} k_{\text{generada}}$

la función PRNG* es un generador de bits que tiene como entrada una semilla (que será la clave de cifrado $k$) y tiene como salida el flujo de bits que aplicaremos sobre el mensaje para cifrarlo con XOR:

$c = k_{\text{generada}} \oplus m$

*) PRNG: Pseudo Random Number Generator

PRNG: seguridad

una hipotética función PRNG es realmente PRNG sii ningún atacante puede distingir entre las dos secuencias:

una generada por una fuente aleatoria "uniforme" (RNG*)
una generada per la hipotética función PRNG

con una probabilidad relevantemente diferente a $\frac{1}{2}$

*) RNG: Random Number Generator (o TRNG) es un sistema que genera una secuencia de bits no predecible sin necesidad de una semilla; no puede implementarse mediante un algoritmo

PRNG: propiedades

equivalentes als RNG:

distribución uniforme (es decir, debe tender a tener el mismo número de 1's que de 0's, tender al mismo número de 00's, que de 01's, 10's...)
despúes de $n$ no se debe poder predecir el $n+1$ con una probabilidad diferente de $\frac{1}{2}$

Obviamente la segunda suponiendo que no se conozca la
semilla del PRNG (la clave de cifrado)

semilla$|k \xrightarrow{\text{PRNG}}$ secuencia pseudo-aleatoria$|k_{\text{generada}}$

Cifrado de flujo: algoritmo

tenemos una función $k \xrightarrow{\text{PRNG}} k_{\text{generada}}$
la función de cifrado es $c = k_{\text{generada}} \oplus m$
la función de descifrado es $m = k_{\text{generada}} \oplus c$

Cifrado de flujo: primer intento

Supongamos que tenemos una función PRNG, y usamos una clave $k$ para cifrar un flujo de datos en una conexión (e.g. TLS)

hemos de vigilar de no reutilitzar $k \xrightarrow{\text{PRNG}} k_{\text{g}}$, si no:

$\begin{aligned} c_1 &= k_{\text{g}} \oplus m_1 \\ c_2 &= k_{\text{g}} \oplus m_2 \\ c_1 \oplus c_2 &= m_1 \oplus m_2 \end{aligned}$

¡hemos eliminado las claves de la ecuación!

(detalle)

$\begin{aligned} c_1 &= k_{\text{g}} \oplus m_1 \\ c_2 &= k_{\text{g}} \oplus m_2 \end{aligned}$

$\begin{aligned} c_1 \oplus c_2 &= (k_{\text{g}} \oplus m_1) \oplus (k_{\text{g}} \oplus m_2) \\ &= k_{\text{g}} \oplus m_1 \oplus k_{\text{g}} \oplus m_2 \\ &= k_{\text{g}} \oplus k_{\text{g}} \oplus m_1 \oplus m_2 \\ &= (k_{\text{g}} \oplus k_{\text{g}}) \oplus (m_1 \oplus m_2) \\ &= (\{000\cdots000\}) \oplus (m_1 \oplus m_2) \\ &= m_1 \oplus m_2 \end{aligned}$

Cifrado de flujo: segundo intento

cambiar las claves en cada transmisión

correcto, pero costoso (poco práctico)

Cifrado de flujo: tercer intento

generar variaciones de las claves en cada transmisión

supongamos que tenemos una función $f$

$\begin{aligned} k' &= f(k, r) \\ {k'}_{\text{generada}} &= \text{PRNG}(k') \\ c &= {k'}_{generada} \oplus m \end{aligned}$

y enviamos cada $r$ juntamente con cada $c$

correcto y práctico

Cifrado de flujo: consideraciones

en resumen: debemos generar un $r$ diferente para cada mensaje
(llamado nonce)

si tenemos una comunicación bidireccional como
HTTPS (TLS) hace falta:

o bien generar un $r$ diferente para cada sentido
o bien generar una $k$ diferente para cada sentido
o ambas $\leftarrow$

Cifrado de flujo: seguridad

el cifrado de flujo es tan seguro como:

será tan seguro como la corrección de la hipótesis de que la función PRNG sea realmente PRNG
el espacio de claves (de semillas) sea tan grande que sea improbable que un ataque de fuerza bruta sea factible
que se cumplan las hipótesis de uso

Ejemplos

RC4 (histórico): obsoleto
ChaCha: derivado del Salsa20 y probablemente la única alternativa al AES en TLS 1.3 (draft)
- $\|k\| = 256$ bit
- $\|\text{nonce}\| = 64$ bit

Cifrados de bloque

Funciones

\[ \begin{aligned} X & = \{ a,b,c,d \} \\ Y & = \{ 1,2,3,4 \} \\ \end{aligned} \\ \]

$f(a) = 1 \quad f(b) = 4 \quad f(c) = 2 \quad f(d) = \text{n.d.}$

por tanto $f$ no es una función sobre $X$
(o al menos no es una función "bien definida" sobre $X$)

\[ \begin{aligned} X & = \{ a,b,c \} \\ Y & = \{ 1,2,3,4 \} \\ \end{aligned} \\ f : X \rightarrow Y \]

$f(a) = 1 \quad f(b) = 4 \quad f(c) = 2$

\[ \begin{aligned} X & = \{ a,b,c \} \\ Y & = \{ 1,2,3,4 \} \\ \end{aligned} \\ f : X \rightarrow Y \\ \]

La función completa es:
$f(a) = 1 \quad f(b) = 4 \quad f(c) = 2$

e.g. la imagen de $b$ es $4$, la preimagen de $4$ es $b$

Todos los elementos de $Y$ que tienen preimagen según $f$ es
$Im(f) = \{1,2,4 \}$

Función biyectiva

todos los elementos de $Y$ tienen preimagen o lo que es equivalente: $Im(f) = Y$ (por tanto, $|X|=|Y|$)

por tanto, la inversa de $f$ (que simbolizaremos $f^{-1}$) está "bien definida"

Función inversa

la función inversa de la anterior $f^{-1}$

todos los elementos de $X$ tienen preimagen

y la inversa de $f^{-1}$ está (obviamente) "bien definida"

por tanto $f^{-1}$ también es biyectiva

permutación

\[ \begin{aligned} X & = \{ a,b,c \} \\ \end{aligned} \\ f : X \rightarrow X \]

una permutación es una función biyectiva de $X$ sobre sí mismo

Cifrado de bloque: modelo

podemos representar el cifrado de bloque con una permutación $f$

$f : X\rightarrow X$

donde $X$ es el conjunto de posibles bloques (tanto de texto en claro como de texto cifrado)

y podemos representar la función de descifrado como su inversa $f^{-1}$

$f^{-1} : X\rightarrow X$

es decir:

$\begin{aligned} c &= f(m) \\ m &= f^{-1}(c) \end{aligned}$

Cifrado de bloque: tamaño de bloque

$\begin{aligned} f &: X \rightarrow X \\ f &: \{0,1\}^n \rightarrow \{0,1\}^n \end{aligned}$

si implementamos $f$ en una tabla con $2^n$ entradas, ocupamos $n·2^n$ bit

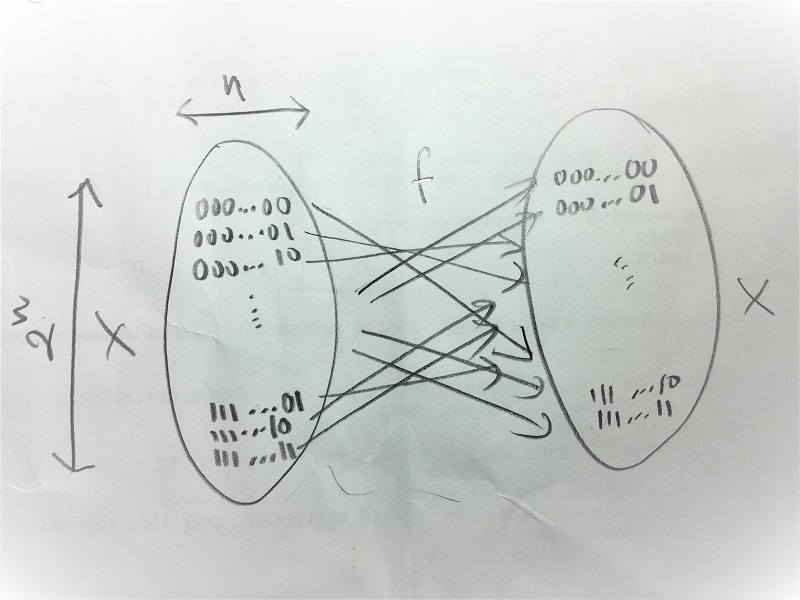
Cifrado de bloque: bloques

si tenemos mensajes más largos que $n$ deberemos de segmentarlos en
bloques de tamaño $n$

Cifrado de bloque: permutación aleatoria

estas $2^{n}$ entradas (de longitud $n$) las deberemos escoger de forma aleatoria

de forma que no podremos conocer $f$ sin conocer la tabla

$\downarrow$

RP: Random Permutation

Cifrado de bloque: modelo

por ejemplo, para DES que tiene un tamaño de bloque de $n=64\text{ b}$ hacen falta:

$64·2^{64} \text{ b} = 2^{70} \text{ b} = 2^{67}\text{ B} = 2^{27}\text{ TB} = 128\text{ EB}$

... para cada una de las claves $k$

obviamente no es factible implementar los cifrados modernos directamente con una tabla indexada

Cifrado de bloque: $f_k$

en realidad para que el cifrado sea seguro necesitaremos una "familia" de funciones equivalentes pero diferentes. Las indexaremos en función de la clave, $k$:

$\begin{aligned} f_k &: X \rightarrow X \\ f_k &: \{0,1\}^n \rightarrow \{0,1\}^n \end{aligned}$

o también, podemos redefinir $f$ y añadirle $k$ como parámetro:

$\begin{aligned} f &: K \times X \rightarrow X \\ f &: \{0,1\}^{\|k\|} \times \{0,1\}^n \rightarrow \{0,1\}^n \end{aligned}$

donde $K$ es el espacio de claves $k$ (o conjunto de claves)

Nota: equivalencia de notación

$f_k : X \color{gray}{\rightarrow X}$	$\longleftrightarrow$	$\color{gray}{y =} f_k(x)$
$f : K \times X \color{gray}{\rightarrow X}$	$\longleftrightarrow$	$\color{gray}{y =} f(k, x)$

Cifrado de bloque:
permutación pseudoaleatoria

igual que para el cifrado de flujo nos hacía falta un flujo de bits aparentmente aleatorio para quien no tuviera la semilla (la clave $k$)...

...para cifrado de bloque utilizaremos permutaciones pseudoaleatorias (PRP*) en les que la permutación será aparentmente aleatoria para alguien que no conozca la clave

esto nos permitirá realizar cifrados de bloque factibles, intercambiando una cantidad inmensa de memoria por una computación abordable

PRP: Pseudo Random Permutation

Cifrado de bloque:
permutación pseudoaleatoria

como en el caso de PRNG, por seguridad hace falta que las PRP sean indistinguibles de las RP

además hace falta que tanto $f_k$ como $f_k^{-1}$ se puedan calcular de forma eficiente

construcción de cifrados de bloque

Cifrados de bloque: clases básicas

hay dos clases de cifrado de bloque
(es decir, dos maneras de implementar PRP)

cifrado de sustitución
- monoalfabéticos ($\approx$ César)
- polialfabéticos (Vigenère)
cifrados de transposición

a partir de ahora utilizaremos $e()$ y $d()$ en lugar
de las $f$ y $f^{-1}$ utilizadas hasta ahora

Cifrados de bloque: composición

por si solas, las 2 clases básicas de cifrado de bloque son inseguras

pero combinandolas podemos obtener seguridad creciente

substitución polialfabética

para un bloque de longitud $t$ elementos, lo que haremos es utilizar $t$ permutaciones $e()$ independentes

$m$	pos1	pos2	pos3	pos4
$c=e(m)$	$f_a($pos1$)$	$f_b($pos2$)$	$f_c($pos3$)$	$f_d($pos4$)$

y simplemente: $d$ es la secuencia de permutaciones inversas $f_i^{-1}$

(el cifrado de Vigenère es un tipo de cifrado de substitución polialfabética)

substitución polialfabética: seguridad

como en el caso de Vigenère podemos recuperar el texto original mediante análisis frecuencial

transposición

para un bloque de longitud $t$ elementos, lo que hacemos es mover los mismos elementos entre sí

por ejemplo, en un sistema con bloque de 4 letras una función $e$ de cifrado podría ser:

$m$	pos1	pos2	pos3	pos4
$c=e(m)$	pos3	pos1	pos4	pos2

y simplemente: $d = e^{-1}$

transposición: seguridad

obviamente son inseguros ya que no solo la frecuencia de los símbolos de entrada se mantiene, si no que los propios símbolos se mantiene (aunque en posiciones diferentes)

composición de cifrados de bloque

una composición de $n$ cifrados de bloque, la podemos escribir:

$\begin{aligned} c_1 &= e_1(k_1, m)\\ c_2 &= e_2(k_2, c_1)\\ &\vdots\\ c &= e_n(k_n, c_{n-1})\\ \end{aligned}$

cada una de las clave $k_i$ puede ser independiente, pero habitualmente se genera en un proceso denominado expansión de clave:

$k \xrightarrow{\text{PRNG}} \{k_1, k_2, \dotsc, k_n\}$

composición de cifrados de bloque:

etapas o rounds: los cifrados de sustitución y transposición se agrupan en parejas y se aplican varias veces (con diferentes claves) hasta obtener un cifrado seguro

$c_i = e_i(k_i, c_{i-1})$

AES

Advanced Encryption Standard

AES

AES es un cifrado de bloque con:

longitud de bloque: $128$ bit ($16$ Byte)
longitud de clave:
- clave de $128$ bit $\implies$ 10 etapas
- clave de $192$ bit $\implies$ 12 etapas
- clave de $256$ bit $\implies$ 14 etapas

AES

cada una de las 10|12|14 etapas se compone de

SubBytes: sustitución de bytes en función de una tabla fija de 256 entradas
ShiftRows: transposición de bytes fija
MixColumns: 4 multiplicaciones modulares de 4 Byte, valores fijos
AddRoundKey: $\text{bloque} \oplus k_{i}$ (subclave $k_{i}$)

esto cifra el bloque, y se pasa al siguiente donde se hace lo mismo pero cambiando la subclave

SubBytes

(fuente Wikipedia)

"sustitución de bytes en función de una tabla fija de 256 entradas"

ShiftRows

(fuente Wikipedia)

"transposición de bytes fija"

MixColumns

(fuente Wikipedia)

"4 multiplicaciones modulares de 4 Byte, valores fijos"

AddRoundKey

(fuente Wikipedia)

"$\text{bloque} \oplus k_{i}$ (subclave $k_{i}$)"

Expansión de clave

Cada una de las etapas (rounds) utiliza una subclave $k_{i}$ diferente

cada una de les subclaves $k_{i}$ se deriva de la clave $k$

Nota 1: las subclaves se aplican ($\oplus$) "alrededor" de las etapas por tanto hace falta una subclave más que etapas hay (11|13|15)

Nota 2: hacen falta más etapas en los AES de clave larga para "aplicar" el mayor espacio de claves sobre el mensaje en claro

AES: vulnerabilidades

...la estadística del mensaje en claro aparece en el texto cifrado igual que en el cifrado del César (!)

ahora los bloques son de $16$ B, no de $1$ B por tanto la estadística es menos importante
($|\text{bloque}|=2^{128}$), pero en secuencias constantes (por ejemplo, como las de un gráfico) se pueden dar bloques enteros idénticos

(fuente Wikipedia)

Un dato cifrado debe parecerse a:

modos de operación

esta "vulnerabilidad" es una propiedad de todos los cifrados de bloque

la contramedida es la misma para todos: no cifrar nunca bloque a bloque, sino cifrar parte del bloque anterior en el bloque actual

este encadenamiento se denomina modo de operación
(y no es opcional)

los modos de operación se deben aplicar a todos los cifrados de bloque

Modos de operación

si acumulamos estado durante el cifrado, podemos utilizar este estado sobre el cifrado del siguiente bloque

ECB: Electronic Code-Book,
- no-op $\Rightarrow$ no se debe utilizar en la práctica (...)
CBC: Cipher Block Chaining
- el bloque $i-1$ se aplica $\oplus$ sobre el bloque en claro $i$
OFB: Output Feedback
- cifras el cifrado anterior, y el resultado $\oplus$ del mensaje en claro
CTR: Counter
- cifras un contador, y el resultado $\oplus$ del mensaje en claro

ECB: Electronic Code-Book

(fuente Wikipedia)

CBC: Cipher Block Chaining

(fuente Wikipedia)

OFB: Output Feedback

(fuente Wikipedia)

CTR: Counter

(fuente Wikipedia)

Vector de inicialización (IV)

los distintos encadenados requieren de una semilla incial, previa, para empezar el encadenado

esto hace que en lugar de transmitir $n$ bloques como en ECB, haga falta transmitir $n+1$

IV en CBC: es el hipotético bloque cifrado $-1$
IV en OFB: es el bloque que se cifra constantmente $e(e(e(\cdots e(\text{IV}))))$ y se aplica sobre los bloques en claro (con $\oplus$)
IV en CTR: es el valor inicial del contador que se cifra ECB, y se aplica sobre los bloques en claro (con $\oplus$)

AES_128_CTR es efectivamente un cifrado de flujo utilizando AES_128_CTR como a PRNG (siendo $k$ la semilla, y el $IV$ el nonce)

AES: rendimiento

Intel, AMD o ARM disponen de instrucciones específicas con el fin de acelerar el des/cifrado AES (y algunos de ellos también tienen instrucciones para GCM)

Según el análisis de 戴维 (Wei Dai) los rendimientos en implementaciones puramente software medidas en Intel Core 2 (2009, MMX/SSE2, 32 b):

AES-128: 1,1 Gbps
AES-192: 0,9 Gbps
AES-256: 0,7 Gbps

bps: bits por segundo (ó b/s)

AES rendimiento comparativo

AES-128: 1,1 Gbps (seguridad 128 bit)
AES-192: 0,9 Gbps (seguridad 192 bit)
AES-256: 0,7 Gbps (seguridad 256 bit)
Salsa20: 3,2 Gbps (seguridad 256 bit)
ChaCha20: 3,2 Gbps (seguridad 256 bit)
AES "hardware": ~8 veces más rápido (Intel, 2011)
DES: 250 Mbps (seguridad 56 bit)
3DES: 100 Mbps (seguridad 112 bit)

bps: bits por segundo

AES: vulnerabilidades

hay distintos ataques que permiten realizar búsquedas de forma más rápida que un ataque de fuerza bruta

AES-128/192/256: recuperación de clave en una quarta parte del tiempo que fuerza bruta $\Rightarrow$ se pierden 2 bits
AES-192/256: sii claves relacionadas, complejidad $2^{119}$ (contramedida: claves aleatorias)
el bloque de $128$ b limita el uso del cifrado hasta $2^{64}$ bloques ($2^{68}$ B) a causa de la paradoja del cumpleaños (contramedida: canviar la clave cuando se haya usado para cifrar $2^{68}$ B)

no son relevantes en cuanto a la seguridad práctica

estas son las vulnerabilidades conocidas...

AES: más vulnerabilidades

AES es público desde el 2000: esto implica un escrutinio público o secreto severo

según los "papeles de Edward Snowden" la NSA está estudiando las vulnerabilidades (no públicamente)

otras "grandes" organizaciones es probable que le dediquen recursos

AES: más vulnerabilidades

algoritmos cuánticos: con el algoritmo de Grover las búsquedas en bases de datos no ordenadas tienen complejidad $O(2^{b/2})$

(obviamente, en computación clásica tiene complejidad $O({2^b})$)

Nota: $b$ son los bits de longitud de la clave AES: $128$, $192$ ó $256$

Computación cuántica

los computadores cuánticos actuales no tienen aplicación práctica: a parte de romper claves sirven para simular... fenómenos de física cuántica
se cree que no habrá computación cuántica práctica antes del ~2030

pero para ser robustos al algoritmo de Grover, sólo hemos de doblar la longitud de claves, por ejemplo pasar a AES-256 daría una fortaleza equivalente de 128 bits

por tanto, se considera que la criptografía simétrica es robusta ante la computación cuántica...

Criptografía simétrica

Criptografía simétrica

Confidencialidad perfecta

Confidencialidad computacional

Confidencialidad computacional

Confidencialidad computacional

Confidencialidad computacional

Confidencialidad computacional

Espacio de claves

NIST

Security Strength

Cuantificación de la Seguridad

Criptografía simétrica

Cifrado de flujo

Cifrado de flujo

Cifrado de flujo

PRNG: seguridad

PRNG: propiedades

Cifrado de flujo: algoritmo

Cifrado de flujo: primer intento

(detalle)

Cifrado de flujo: segundo intento

Cifrado de flujo: tercer intento

Cifrado de flujo: consideraciones

Cifrado de flujo: seguridad

Ejemplos

Cifrados de bloque

Funciones

Función biyectiva

Función inversa

permutación

Cifrado de bloque: modelo

Cifrado de bloque: tamaño de bloque

Cifrado de bloque: bloques

Cifrado de bloque: permutación aleatoria

Cifrado de bloque: modelo

Cifrado de bloque: $f_k$

Nota: equivalencia de notación

Cifrado de bloque: permutación pseudoaleatoria

Cifrado de bloque: permutación pseudoaleatoria

construcción de cifrados de bloque

Cifrados de bloque: clases básicas

Cifrados de bloque: composición

substitución polialfabética

substitución polialfabética: seguridad

transposición

transposición: seguridad

composición de cifrados de bloque

composición de cifrados de bloque:

AES

AES

AES

Expansión de clave

AES: vulnerabilidades

modos de operación

Modos de operación

Vector de inicialización (IV)

AES: rendimiento

AES rendimiento comparativo

AES: vulnerabilidades

AES: más vulnerabilidades

AES: más vulnerabilidades

Computación cuántica

(Hash) $\rightarrow$

Cifrado de bloque:
permutación pseudoaleatoria

Cifrado de bloque:
permutación pseudoaleatoria